GNU mini-gmp Library ported to arduino. Now I am able to genarate rsa Key(512) bits

[tiny]

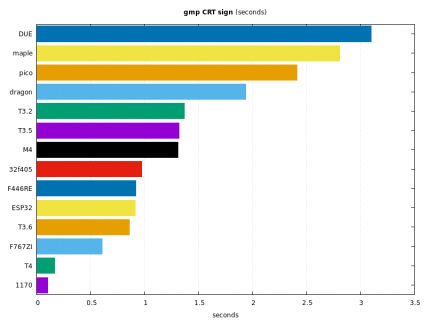
Now I can generate a 512 bit rsa keypair in 2278 ms on a Tennsy 3.2
Crypting a 110 byte message costs 17ms, decrypting 856ms.

Well this library is not C++, just C, but in contrast to BigNumber Library the Integers are stored in binary instead of BCD so it's faster and consumes less memory.
Here a short example of generating a keypair:

/* **************************************************************************************** */
void generate_keys(private_key* ku)
{

    char buf[BUFFER_SIZE];
    int i;
    mpz_t phi; mpz_init(phi);
    mpz_t tmp1; mpz_init(tmp1);
    mpz_t tmp2; mpz_init(tmp2);

    mpz_set_ui(ku->e, 65537); 

    for(i = 0; i < BUFFER_SIZE; i++)
        buf[i] = random(255) % 0xFF; 
    buf[0] |= 0xC0;
    buf[BUFFER_SIZE - 1] |= 0x01;
    mpz_import(tmp1, BUFFER_SIZE, 1, sizeof(buf[0]), 0, 0, buf);
    mpz_nextprime(ku->p, tmp1);
    mpz_mod(tmp2, ku->p, ku->e);        /* If p mod e == 1, gcd(phi, e) != 1 */
    while(!mpz_cmp_ui(tmp2, 1))         
    {
        mpz_nextprime(ku->p, ku->p);    /* so choose the next prime */
        mpz_mod(tmp2, ku->p, ku->e);
    }
    do {
        for(i = 0; i < BUFFER_SIZE; i++)
            buf[i] = random(255) % 0xFF; 
        buf[0] |= 0xC0;
        buf[BUFFER_SIZE - 1] |= 0x01;
        mpz_import(tmp1, (BUFFER_SIZE), 1, sizeof(buf[0]), 0, 0, buf);
        mpz_nextprime(ku->q, tmp1);
        mpz_mod(tmp2, ku->q, ku->e);
        while(!mpz_cmp_ui(tmp2, 1))
        {
            mpz_nextprime(ku->q, ku->q);
            mpz_mod(tmp2, ku->q, ku->e);
        }
    } while(mpz_cmp(ku->p, ku->q) == 0); /* If we have identical primes (unlikely), try again */

    mpz_mul(ku->n, ku->p, ku->q);

    mpz_sub_ui(tmp1, ku->p, 1);
    mpz_sub_ui(tmp2, ku->q, 1);
    mpz_mul(phi, tmp1, tmp2);

    if(mpz_invert(ku->d, ku->e, phi) == 0)
    {
        mpz_gcd(tmp1, ku->e, phi);
        sprintf(sbuf,"gcd(e, phi) = [%s]\n", mpz_get_str(NULL, 16, tmp1));
        Serial.print(sbuf);
        sprintf(sbuf,"Invert failed\n");
        Serial.print(sbuf);
    }
    mpz_clear(phi);
    mpz_clear(tmp1);
    mpz_clear(tmp2);
    return;
}

I'am willing to publisch the entire code, is somebodey interseted

 

[manitou]

Re: mini-gmp

I just copied the .c and .h files from https://github.com/Cl3Kener/gmp/tree/master/mini-gmp into my sketch folder and was able to compile and run various big-integer tests. Big number arithmetic is the limiting performance factor in public key cryptography (RSA and Diffie-Hellman). I have some comparative numbers on various MCUs for calculating 100! with various multiprecision arithmetic libs. See
https://github.com/manitou48/DUEZoo/blob/master/perf.txt
The mini-gmp lib is much faster than the old Arduino BigNumber lib, but the wolfssl lib seems to be the fastest for the 100! test.

mini-gmp performance (microseconds):

     gmp         100!    DH       RSAs    RSAv   CRT     us    Faster
     T4            32   118834   596073   4674  167372  @600mhz
     T3.6         154   613554  3046753  23929  857665  @180mhz
     T3.5         244   942554  4633162  36401 1322092  @120mhz
     T3.2         253   971358  4714782  37047 1367517  @120mhz
     ESP32        269   649007  3199366  25175  913197  @240mhz -O2
     M4           277   949511  4694184  36870 1311418  @120mhz  SAMD51
     32F405       191   696230  3440666  27021  971729  @168mhz -O2
     F446RE       166   658182  3255084  25556  916767  @180mhz -O3
     F469NI       166   658188  3255096  25556  916778  @180mhz -O3
     F767ZI       110   436642  2171996  17050  607406  @216mhz -O3
     dragon       358  1383216  6785372  53320 1937244  @80mhz
     maple        529  2020175  9982062  78379 2808196  @72mhz  -O2
     DUE          503  2226100 11074698  87039 3098825  @84mhz  -Os
     ZERO/cpx    1171  4821906 23857807 187264 6716343  @48mhz  -Os SAMD21
     R4           713  2388621 11783349  92539 3301502  @48mhz  -O3
     pico         415  1739322  8682992  68165 2414692  @125mhz -O3
     1010          67   122292   605772   4759  605772  @500mhz -O3
     1170          57    75439   373023   2932  104778  @996mhz -O3 SDK

See wolfssl/mbedtls and RSAsign results here. We use the same 2048-bit RSA key as the wolfssl/mbedtls tests. DH uses 1024-bit integers.