Acoustic Echo Cancelation(AEC)

Status
Not open for further replies.
S

snirtikam

Member
Hello,
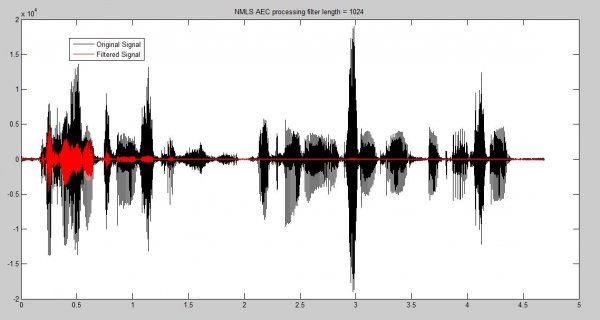
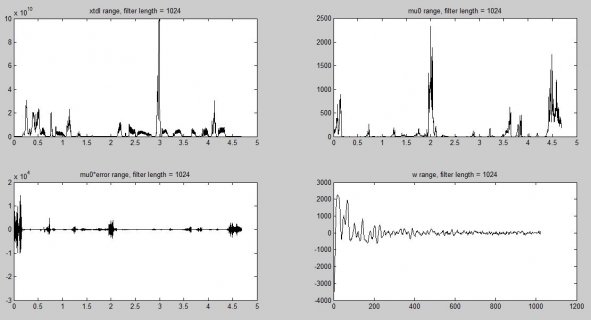
I'm hoping to get some help with this. What i'm implementing is AEC between two teensy boards and using Audio shield. So, to get rid of echo, I have to compare incoming audio signal from far end teensy and microphone and do some processing (i know how to do that part). What i'm having trouble with is retrieving sampled data from the microphone for manipulation. I know data is sampled at 44.1kSps in blocks of 128, which is about 2.9ms, but how to retrieve that data block as a double or int data is what i dont understand how to do. I've looked over 'Recording' example and in that example 'readBuffer()' returns a pointer to 128 block and then a 512 byte buffer is filled. How can i get that data and maybe cast is as double, or int... ? Is that possible? Any help, suggestions would be awesome.

Thank you!
 
The reference documentation for this (and all objects in the audio library) can be found in the design tool's right-side panel.

http://www.pjrc.com/teensy/gui/?info=AudioRecordQueue

snirtikam said:
I've looked over 'Recording' example and in that example 'readBuffer()' returns a pointer to 128 block and then a 512 byte buffer is filled. How can i get that data and maybe cast is as double, or int... ?
Click to expand...

readBuffer() give you an array of int16_t data.

So you could do something like this:

Code: 
  int16_t *data = queue1.readBuffer();

  Serial.println(data[0]);    // the first sample
  Serial.println(data[128]);  // the last sample

  queue1.freeBuffer();        // do not use "data" after this!
 
Thank you very much for your quick response. I've tried your suggestion, but I'm a little confused by the output. The 'data' is printing samples of of the 128 array and they way i had it set up is that i'm sampling from microphone and printing all 128 sample in a 'for' loop. However, all of the printed samples are the same, and there are bunch of zeros ... Not sure what i'm doing wrong. If queue is filled with sample from microphone should they be somewhat random? Another question, does each sample represent 16 bit voltage from ADC from -1/+1 volts? Little confused on this... Any help/input is greatly appreciated. Thank you!

my screen capture of serial monitor:
dataOut.JPG
my code:

//
// Microphone to Speaker output

#include <Audio.h>
#include <Wire.h>
#include <SPI.h>
#include <SD.h>
#include <SerialFlash.h>


// GUItool: begin automatically generated code
AudioInputI2S Mic; //microphone
AudioRecordQueue MicMem; //queue for microphone
AudioOutputI2S headphones; //output
AudioConnection patchCord1(Mic, 0, MicMem, 0);
AudioConnection patchCord2(Mic, 0, headphones,0);
AudioConnection patchCord3(Mic, 0, headphones,1);
AudioControlSGTL5000 sgtl5000_1; //xy=339.6666564941406,285.6666488647461
// GUItool: end automatically generated code
int16_t data1[128];


const int micInput = AUDIO_INPUT_MIC;

void setup() {
Serial.begin(9600);
AudioMemory(20);
sgtl5000_1.enable();
sgtl5000_1.volume(0.5);
sgtl5000_1.inputSelect(micInput);
sgtl5000_1.micGain(36);
delay(1000);
}

void loop() {
MicMem.begin();
int16_t *data = MicMem.readBuffer();

for(int i = 0; i < 128; i++) {
Serial.println(data);
}
MicMem.freeBuffer(); // do not use "data" after this!
MicMem.end();
delay(500);
}
 
Last edited:
My apologies. Thank you for posting reply. I've read over the Recorder example but that is of no help to me because it writes the data to SD card and plays the .wav. I just want the raw data samples from the buffer and I cant seem to get that.
 
Yes, it writes the Data. So, it gets them :)
It shows how to access the data, the usage of "MicMem".begin(); MicMem.end(); MicMem.readBuffer();" and much more. Try to "read" it.

AEC will be *much* more difficult than this...
 
Is automatic echo cancellation (AEC) normally done as I'm accustomed to in RF? Adaptive equalization? For each frequency range A to B, amplitudes in that range are inverted and summed to cancel. The hard part of course is one-tie training for a particular room/auditorium, or real time adaptive. In RF, such as DOCSIS and other than OFDM, the adaptive equalizer finds the earliest direct signal in the time span, then finds that same weaker signature in a later time or times. Lots of DSP work. A fixed, non-adaptive (one time training, e.g,. after the room's arrangement is settled (sets in place, simulated audience), the equalizer inverse can be observed and retained. Much simpler. But some applications need adaptive.

In RF, adaptive equalizers reduce the affect of multipath (RF echos if you will). It's key to faster forms of DOCSIS (cable modems) and in some forms of cellular, mostly older TDMA (not spread spectrum/OFDM in LTE).

I apologize if this seems off the audio theme, but the principles are the same.
 
Thank you for information. I'm not quite certain how automatic echo cancellation is done in RF, but what i was referring to is Acoustic Echo Cancellation. The two might be the same. I've implemented AEC in real time using Frequency Blocking Least-Mean Square (FBLMS) algorithm between two laptops using MATLAB via TCP/IP connection. However, MATLAB is not optimized for real-time processing, it is quite slow. There are many other algorithms that can be implemented but due to slower processing of MATLAB, FBLMS algorithm worked best for real time processing. My next step was to implement this on FPGA or some dev board and Teensy seemed like a good option. As far as algorithm goes, I know how to implement that and have a code written already, but for that i need samples from the microphone and a signal that coming from the microphone of another teensy so that i can run both through algorithm and send the result out to the other teensy.
So far i've been having trouble getting sampled data from microphone. It has been a while since i've done C/C++ programming in embedded systems so i'm trying to catch up with a lot of things here. At this point I have two teensy boards and i've been able to establish communications between both via WIFI chips (can send data both ways).

I've been studying "Recording" example, but, as I said, it has been a while with embedded programming and its a challenge.

Thanks for the input. I appreciate it.
 
Hello All,

So i've been able to make little progress on this project. To test the echo cancellation algorithm i've chosen to use simple NLMS algorithm. the way i'm testing this algorithm is i'm running the set up on one teensy and sending mic signal to both inputs of NLMS algorithm, far side and near side. The code works, but the problem i'm having is that I'm not sure how to make it faster, or keep up with teensy's sampling. I've posted code bellow.

Basically, because of 'for' loops the NLMS algorithm takes long to process one block of audio samples. 1 block is about 2.9 ms of time, but running code in real time takes longer. As a result, the output to speaker is choppy because NLMS code has to complete before audio starts sampling again. I'm looking for some advice on how to implement it smarter, or mayby i'm approaching this wrong way. Any advice would be greatly appreciated.

Code: 
// 
// Microphone to Speaker output
#define NUMEL(x) (sizeof(x)/sizeof((x)[0])) // retuns/calculates the size of an array

//#include "NLMS.h"
#include <Audio.h>
#include <Wire.h>
#include <SPI.h>
#include <SD.h>
#include <SerialFlash.h>

//*****functions**********
void getBuffer1();
void playData();
void displayData();
void NLMS_AEC();

// GUItool: begin automatically generated code
AudioInputI2S            Mic;           //microphone
AudioPlayQueue           MicMem;         //queue for microphone
AudioRecordQueue         Memory;
AudioOutputI2S           headphones;           //output
AudioConnection          patchCord1(Mic, 0, Memory, 0);
AudioConnection          patchCord2(MicMem, 0, headphones,0);
AudioConnection          patchCord3(MicMem, 0, headphones,1);
AudioControlSGTL5000     sgtl5000_1;     //xy=339.6666564941406,285.6666488647461

const int numBlocks = 2; //min block size is 2!!!!!!
const int lFilt = numBlocks-1;
const int gg = lFilt*128;
int16_t *pAddr; //pointer to 128 block of getBuffer
int16_t lblock = numBlocks*128; //length of arrays
int16_t ablock[128*numBlocks];  // set an array block
int16_t *pablock; // pointer to an array block
int16_t *pp; // pointer to getBuffer
int n;
unsigned long time1; // time variable


//***************NMLS const and settings*************************
const int16_t numTaps = gg;
float mu = 0.0001;
float mu0 = 0;
float psi = 0.0001;
float w[numTaps];
float *pw; // pointer to w 
float yhat = 0;
float xtdl = 0;


//define input/source
const int micInput = AUDIO_INPUT_MIC;

void setup() {
  memset(w,0,numTaps);
  memset(ablock,0,128*numBlocks);
  //initialize pointers for NLMS
  pw = w;
  Serial.begin(115200); // initiate baud rate for serial comm.
  AudioMemory(8); // allocate # of audio memory (each block has 128 sample of data)
  sgtl5000_1.enable(); // enalbe 
  sgtl5000_1.volume(0.5); // output volume
  sgtl5000_1.inputSelect(micInput); //input selection (mic or line in)
  sgtl5000_1.micGain(36); // mic gain
  //set array values to zero
  pablock = ablock; // assign pointer to array
  delay(1000);
}


//***************************MAIN LOOP********************************************************************
void loop() {
getBuffer1(numBlocks); //returns pointer to the buffered data
//print sample to serial plotter 
//displayData(pablock); // print data to serial plotter
NLMS_AEC(pablock,pablock,pablock,pw,gg,.0001);
}



//*********************************************************************************************************
// print data to serial plotter
void displayData(int16_t * data){
  for(int i = 0; i<128*numBlocks;i++){
  Serial.println(*(data+i));
}
}
// play data to speaker
void playData(int16_t *data, int i){
    pAddr = MicMem.getBuffer(); //get pointer to 128 array playBuffer 
    // take one block from buffer array (ablock) and copy it to playBuffer pointer
    // play that block
    memcpy((byte*)pAddr,(byte*)data+(256*i),256);
    MicMem.playBuffer();
}

// buffer an array with samples from Microphone
// function receives and array and integer indicating number of blocks
void getBuffer1(int x) {
  Memory.begin(); // begin putting sample data into memory
  int l = 0;
  memcpy((byte*)pablock,(byte*)pablock+256,256*(x-1));
  // put 128 blocks of sample into an array size of 128*(number of blocks)
    while(l == 0){ // wait until block samples are available
      if(Memory.available() ==1) {// if availabe copy 128 block to array and get out of while loop      
        //read one 128 block of samples and copy it into array
        memcpy((byte*)pablock+(256*(x-1)),Memory.readBuffer(),256);
        Memory.freeBuffer(); // free buffer memory
        //NLMS_AEC(pablock,pablock,pablock,pw,gg,.0001);
        playData(pablock,(x-1)); // play 128 block from buffered array
        l = 1; // set n to 1 to get out of while loop
      }//end if 
    }//end while 
    l = 0;
   //Memory.clear(); // clear all audio memory 
   Memory.end(); // end memory capture
//   return ablock; // regurn pointer to array
}

// NMLS algorithm
// inputs are Mic Signal, far end signal and index of n-1 block wher n is the current block itteration
// previous block data is used to modify current block data samples
void NLMS_AEC(int16_t *Mic, int16_t *x){
  for(int h = 0; h<128;h++){
    for(int j = gg; j >0;j--){
      yhat = yhat+x[j+h]*pw[gg-j];
    }
    pablock[h+gg] = (int16_t)(Mic[gg+h]-yhat);
    yhat = 0;
    
    for(int j = gg; j >0;j--){
      xtdl = xtdl+x[j+h]*x[j+h];
    }
    xtdl = xtdl + psi;
    mu0 = mu/xtdl;
    xtdl = 0;
 
    //update filter taps
    for(int j = 0; j<gg;j++){
      pw[j] = pw[j] + x[gg-j+h]*mu0*pablock[h+gg];
    }//end for
  }//end for outer
}// end NLMS_AEC
 
You're probably going to have to replace these floating point numbers with fixed point.

Code: 
float mu = 0.0001;
float mu0 = 0;
float psi = 0.0001;
float w[numTaps];
float *pw; // pointer to w 
float yhat = 0;
float xtdl = 0;

Before beginning this journey, you really should try to verify the math is connect with the floats. After converting to fixed point, it's much harder to change the math. In fact, some sorts of algorithm changes are probably best done by going back to floats, and then redoing the float to fixed conversion after you're sure the algorithm is correct.

The first step is determining the numerical ranges your floats actually use. The w[] array is probably the most important. The 2 ways involve carefully analyzing the equations, or just running a large amount of real data and collecting min/max with a little extra code. In extreme cases, you might log all the numbers and plot a histogram, to learn whether the numbers are uniformly distributed or if there's some unusual usage, like some cases really large numbers, others very small.

After you know the range, you choose an integer that will represent the number. For example, if you learn those w[] coefficients range from -1.7 to +1.7 with fairly uniform distribution, perhaps you'd choose a 3.13 format. The 3 top bits of an int16_t would represent the numbers +1 to -2. The bottom 13 bit represent the fraction. So the number 1.4 would be 001 in the top 3 bits, and 0110011001101 (integer 3277) in the lower 13 bits. To understand the fractional part, consider 13 bits is 8192 integers. Divide 3277 by 8192 and you get 0.4000244. Or if you divide the whole 16 bit number (11469) by 8192, you get 1.4000244. Of course, you can choose scaling by any arbitrary integer, but powers of 2 are commonly used so you know certain bits are the whole number part and the other bits are the fraction part.

Generally you'd try to use 16 bit numbers for the coefficients, if the round-off errors are tolerable. Usually you'd use int32_t or even int64_t for calculated values. For example:

Code: 
      yhat = yhat+x[j+h]*pw[gg-j];

For this code, you'd almost certainly use int64_t for yhat. The multiply will produce an int32_t, and when you add 128 of them together the result can easily become larger than 32 bits. Fortunately, Teensy has fast instructions for accumulating to 64 bit integers.

Then after the loop, you'd add code to convert the 64 bit result to something more useful. Often the conversion is as simple as right shifting to throw away the lower bits.

Usually when doing this sort of conversion, it helps to keep the float code and do both calculations. That's even slower, but the idea is you can do them both and add a little code to compare if they ended up with the same answer (plus or minus a tiny extra error due to round-off issues). Then when it's all working nice, delete or comment out the float code.

After the integer stuff is working, there's a second round of possible optimizations you can do with the Cortex-M4 DSP extensions. But that's quite complex, so usually your first goal should be converting from float to all int in the simplest way you can.

Hopefully this help?

Do you believe this echo cancel might be worth contributing to the audio library? Is the code open source?
 
Hello,

Thank you for your response. I've tried your suggestion and just experimented with int16_t and int32_t and it cuts the processing time from 60ms to about 33ms. Now that is using a filter length of 640 which is about 5 blocks, roughly 14.5ms. The length of the filter comes from assuming that the device is in 12x12 foot room and given the speed of sound, return time from speaker back to microphone (bouncing off walls) will be about 14ms. Now that is minimum. Typical filter have lengths of more than 1024, depending on the environment. So, I still have a little bit of bottle neck here.... One way I though of dealing with this is to use lower sampling rate. Typical speech doesn't require 44.1ksps, so i though to cut that to 10.025ksps... I'm not sure how easy it would be to do that in audio shield library/hardware files. I was looking through "SGTL5000" files in audio library and there is something about setting sampling rate and clock rate, but i'm not sure if it would be that simple.

As far as the code, I'm assuming you are asking about NLMS or just overall, its open source. And, as far as contributing to audio library, I think it would be good. I'll be happy to share anything I'll have.
 
Last edited:
Ok, that's good progress. We only need another 5X speedup! Let's look at the DSP extensions first. :)

If this is going to be an open source contribution, and if I'm going to work on the DSP instruction speedups, I really need you to put this on github. If you've never used git & github before, there's lots of beginner tutorials. Especially git has some incredibly powerful but complex features, which you don't need. I use it every day and I don't have much idea how all that stuff works. All you really need to know is how to create a free account, create a new repository with your code, and then how to push changes from your PC to github, and how to pull contributions (like DSP speedups from me) you've merged on github down to your PC.

Well, the one obvious caveat to collaborating on github is to push your changes up to github regularly, even if they're unfinished, so I'm not try to work with an old version. Of course, also merge pull requests and pull the changes into your copy before starting new work, so you're working on the latest code too.

Hopefully you can do a couple simple things in the code...

1: If possible, please try to create at least 1 test that uses recorded or synthesized signals rather than live input. As I try to convert parts of the code to use the DSP extensions, having tests we can both run that produce known results will really help. It'll also help for an example to add to the library.

2: Please add an open source license. The Teensy Audio Library is MIT license, so it really needs to be MIT or something very close. Use your name, and the names of anyone else who wrote any substantial part of the code (of course with their consent to publish it with this open source license). If possible, please also add links or references to info you used for the algorithm. As part of an open source library that people will very likely use in non-profit and commercial projects, there needs to be at least some documentation that the author(s) allow the code to be open source, and in the case of complex algorithms how they were developed. If there's any published papers or articles or books older than 21 years, a reference to such "prior art" is really nice. No need to create a detailed bibliography, just URLs or casual references are fine.

Let me know when it's up on github? I'll take a look and see if I can apply the DSP extensions....
 
Last edited:
Hello Paul,

I have heard of github, but have never used on myself. My partner, with whom I work on this does have an account so we'll be able to provide that to you. This is my first time doing open source license stuff, or MIT license, so I'll read up on that to get more familiar with your instructions.

Some success though....
I fallowed your advice from earlier post about getting rid of floats, and I'm happy to say that I was able to convert everything to be with types int16_t and one int64_t. Converting sped up the processing time drastically. I implemented the changes in NLMS and tested it. Happy to say it works in real time processing. However, that is only with filter length of 128. Increasing filter length makes output choppy due to delay in processing. Below is my code and plots of ranges of variables withing NLMS algorithm.

here is my updated code (I will work on getting the github going, promise)
Code: 
// 
// Microphone to Speaker output
#define NUMEL(x) (sizeof(x)/sizeof((x)[0])) // retuns/calculates the size of an array

#include "NLMS.h"
#include <Audio.h>
#include <Wire.h>
#include <SPI.h>
#include <SD.h>
#include <SerialFlash.h>

//*****functions**********
void getBuffer1();
void playData();
void displayData();
void NLMS_AEC();

// GUItool: begin automatically generated code
AudioInputI2S            Mic;           //microphone
AudioPlayQueue           MicMem;         //queue for microphone
AudioRecordQueue         Memory;
AudioOutputI2S           headphones;           //output
AudioConnection          patchCord1(Mic, 0, Memory, 0);
AudioConnection          patchCord2(MicMem, 0, headphones,0);
AudioConnection          patchCord3(MicMem, 0, headphones,1);
AudioControlSGTL5000     sgtl5000_1;     //xy=339.6666564941406,285.6666488647461

const int numBlocks = 2; //min block size is 2!!!!!!
const int lFilt = numBlocks-1;
const int gg = lFilt*128;
int16_t *pAddr; //pointer to 128 block of getBuffer
int16_t lblock = numBlocks*128; //length of arrays
int16_t ablock[128*numBlocks];  // set an array block
int16_t error[128]; 
int16_t *Perror;
int16_t *pablock; // pointer to an array block
int16_t *pp; // pointer to getBuffer
int n;
unsigned long time1; // time variable


//***************NMLS const and settings*************************
const int16_t numTaps = gg;
int16_t mu = 13;
int16_t mu0 = 0;
int8_t psi = 1;
int16_t w[numTaps];
int16_t *pw; // pointer to w 
int16_t yhat = 0;
int64_t xtdl = 0;


//define input/source
const int micInput = AUDIO_INPUT_MIC;

void setup() {
  memset(w,0,numTaps);
  memset(ablock,100,128*numBlocks*2);
  memset(error,0,128);
  //initialize pointers for NLMS
  pw = w;
  Perror = error;
  Serial.begin(9600); // initiate baud rate for serial comm.
  AudioMemory(8); // allocate # of audio memory (each block has 128 sample of data)
  sgtl5000_1.enable(); // enalbe 
  sgtl5000_1.volume(0.5); // output volume
  sgtl5000_1.inputSelect(micInput); //input selection (mic or line in)
  sgtl5000_1.micGain(26); // mic gain
  //set array values to zero
  pablock = ablock; // assign pointer to array
  delay(1000);
}


//***************************MAIN LOOP********************************************************************
void loop() {
//Serial.println(millis()); // print time 
getBuffer1(numBlocks); //returns pointer to the buffered data
//print sample to serial plotter 
//displayData(pablock); // print data to serial plotter
//NLMS_AEC(pablock,pablock);
//for(int i = 0; i<128;i++){
//  Serial.println(w[i]);
//}
}
//*********************************************************************************************************
// print data to serial plotter
void displayData(int16_t * data){
  for(int i = 0; i<128*numBlocks;i++){
  Serial.println(*(data+i));
}
}
// play data to speaker
void playData(int16_t *data, int i){
    pAddr = MicMem.getBuffer(); //get pointer to 128 array playBuffer 
    // take one block from buffer array (ablock) and copy it to playBuffer pointer
    // play that block
    memcpy((byte*)pAddr,(byte*)data+(256*i),256);
    MicMem.playBuffer();
}

// buffer an array with samples from Microphone
// function receives and array and integer indicating number of blocks
void getBuffer1(int x) {
  Memory.begin(); // begin putting sample data into memory
  int l = 0;
  memcpy((byte*)pablock,(byte*)pablock+256,256*(x-1));
  // put 128 blocks of sample into an array size of 128*(number of blocks)
    while(l == 0){ // wait until block samples are available
      if(Memory.available() ==1) {// if availabe copy 128 block to array and get out of while loop      
        //read one 128 block of samples and copy it into array
        memcpy((byte*)pablock+(256*(x-1)),Memory.readBuffer(),256);
        Memory.freeBuffer(); // free buffer memory
//        NLMS_AEC(pablock,pablock);
//        playData(Perror,0); // play 128 block from buffered array
        l = 1; // set n to 1 to get out of while loop
      }//end if 
    }//end while 
    NLMS_AEC(pablock,pablock);
    playData(Perror,0); // play 128 block from buffered array
    l = 0;
   Memory.clear(); // clear all audio memory 
   Memory.end();
//   return ablock; // regurn pointer to array
}

// NMLS algorithm
// inputs are Mic Signal, far end signal and index of n-1 block wher n is the current block itteration
// previous block data is used to modify current block data samples
void NLMS_AEC(int16_t *Mic, int16_t *x){
  for(int h = 0; h<128;h+=1){
    for(int j = gg; j>0;j-=1){
      yhat += (x[j+h]*pw[gg-j])/32768;
      xtdl += x[j+h]*x[j+h];
    }
    error[h] = Mic[gg+h]-yhat;
    yhat = 0;
    xtdl = xtdl + psi;
    mu0 = (67108864*mu)/xtdl;
    xtdl = 0;
 
    //update filter taps
    for(int j = 0; j<gg;j+=1){
    pw[j] = pw[j] + (x[gg-j+h]*mu0*error[h])/131072;
    }//end for
  }//end for outer
}// end NLMS_AEC
int16NLMinputvsoutput.JPG
int16NLMSranges.JPG
 
That's great news!

I have some ideas for this code which should give you another large speed increase.

Github recently added the ability to just drag-and-drop files from your PC into the web page, so no software install needed. Very easy. It's free to sign up and create public projects (they only charge if you want to keep your data private - like a company developing code they don't share). I know it's some trouble to learn yet another website, but this really is important for sharing the code.

Let me know when it's on github?

Also, please try to make a copy that plays a pre-recorded sample. That way I can test with the exact same sound. For an example, look at Duff's NoteFrequency program:

https://github.com/PaulStoffregen/Audio/tree/master/examples/Analysis/NoteFrequency

Those other files are sound clips, converted to C code using the wav2sketch program.

https://github.com/PaulStoffregen/Audio/tree/master/extras/wav2sketch
 
I believe the DSP extensions can make a massive speed increase for these 2 loops:

Code: 
                for (int j = gg; j > 0; j -= 1){
                        yhat += (x[j+h]*pw[gg-j])/32768;
                        xtdl += x[j+h]*x[j+h];
                }

The yhat variable will become int64_t (yes, that will actually be faster) with the 15 bit shift done only once after the loop.

Code: 
                for(int j = 0; j<gg;j+=1){
                        pw[j] = pw[j] + (x[gg-j+h]*mu0*error[h])/131072;
                }

The DSP extensions can be used with 32 bit data packing and the successive memory fetch optimization and partial loop rolling, which gets the data from the arrays much faster, and then does the math much faster. The chip has 2 operation SIMD which can be used in this case. The details are complicated... so it's important to get this code correct before making the difficult conversion to the DSP extensions. It will make a tremendous speed increase!

Let me know when this is on github with a MIT license, and I'll work on the speedup part.
 
Hi Paul,

'We got the github going. Added files and license stuff. Here is the link: https://github.com/kfillerup/NLMS_AEC

I also added NLMS.h file with the algorithm code. Working on the sound file. Is there an example of how to use the wav2sketch.c file? I use MATLAB a lot, so I can make a speech recording on it at different sampling rates and/or format types.

Thanks.
 
wav2sketch is a command line program, so you must run it in a terminal (Mac, Linux) or command prompt (Windows). First, type "cd" commands to change to the directory where you have WAV files for sound clips. The WAV files must be 44, 22 or 11 kHz. Then type either "wav2sketch" or "wav2sketch -16". The first uses ulaw compression. Adding "-16" preserves the 16 bit data, but at the cost of larger memory usage. It will read all the WAV files in the current directory and convert them all the .c and .h files.
 
"gg" is 128 (minimum), there are two loops of it which means 2*128 =256 loops per sample, 128*256 per block(=32768). Is there a way to save some iterations ?
 
'gg' is the index location of the last block in the 'Mic' and 'x' array. so lets say we have a filter length of 128, this means that 'Mic' and 'x' need to be length of 256 and gg = 128. If filter length is 1024, then gg = 1024 and 'Mic' will have to be length of 1024+128. The outer 'for' loop, in NLMS, will always calculate 1 block of data, which is an array of 128. This block of data is calculated using past samples: length of past sample has to be same as length of filter. That block of data will be stored in error array and sent out to speaker, in my case, or to the far side speaker (the speaker of the other teensy). error array will always be lenth of 128, however length of filter will change, which will change length of 'Mic' and 'x' array. So, I don't think that there is away of avoiding iterations. what i have in NLMS is the minimum that would be needed to calculate error array. Now, as far as I understand some optimizations can be done to make this more efficient in DSP.
 
At 96 MHz, we get 100% CPU usage at approx 2000 cycles per sample. So ultimately that's going to impose a limit on how many iteration are possible.

I'm going to make a first attempt at using the DSP extensions, so we can see how many cycles/iteration are really needed...
 
Frank B said:
perhaps unrolling the outer (variable h) loop.. by two or four
Click to expand...

..could help, and even if it is only to use combined loads and stores (which are more efficiant)

for example
Code: 
    for(int j = gg; j>0;j-=1){
        yhat += (x[j+h]*pw[gg-j])/32768;
 xtdl += x[j+h]*x[j+h];
    }
could do 2 or more iterations of h (correct me)
Code: 
    for(int j = gg; j>0;j-=1){
        pwt = pw[gg-j];
 xt = x[j+h];
 xt1 = x[j+h+1]; //combine reads, saves cpu cycles on ARM-CM4
 yhat += (xt*pwt)/32768;
 yhat1 += (xt1*pwt)/32768;
 xtdl += xt*xt;
 xtdl1 += xt1*xt1;
    }

then, it may be more efficiant to calculate (67108864*mu) only once and not in every iteration
(and of course xtdl and so on should be used as temporary local variables.

edit: and doing the loop from above backwards with do..while means 1 cycle less per iteration (= 128*128 cycles for a block)
edit:gcc does no automatic loop-unrolling with -Os or -O1, not even automatic inlining...
 
Last edited:
Would this algorithm still work well enough if the w[] array were half the size and each filter tap applied to 2 audio samples?

Edit: some good recorded test cases would really help for collaborating....
 
Last edited:
Hi Frank,
Thank you for suggestion. I'm not sure though that that will work for AEC part. It might be efficient as far as saving iterations, but not for the algorithm. In the code
Code: 
 pw[j] = pw[j] + (x[gg-j+h]*mu0*error[h])/131072;
mu0 is the result of multiplication (mu*67108864)/xtdl, where xtdl is the mean taken from signal 'x' and it has to be computed before using it in filter update equation, otherwise NLMS algorithm wont work. So xtdl = x[gg:-1:0]'*x[gg:-1:0] where gg is the length of filter and " ' " is the transpose of vector 'x'. This, again, has to be calculated before being used in filter tap weights "pw" update.

Another thought I had on how to buy some time is to do NLMS calculations in between sample acquisition and also running at slower sampling rate. Here is what i mean. Currently we have 1 block of data being filled, which equals to 2.9ms of time. With a block of 128 we have 22.67 microseconds between samples. We can run NLMS algorithm in between each sample and the outer 'for' loop will run only once instead of 128 times. We can also buy more time by sampling at lower rate. For example if we sample at 10.025ksps we'll have 99.75 microseconds in between each sample and running NLMS for just 1 sample will give us needed time. I'm not sure how difficult it will be to do that, but at 10.025ksps 1 block of data will be ready every 12.76ms and NLMS will run for single sample instead of 128. Just a thought.
 
For example, can something like this work?

Code: 
  for(int h = 0; h < 128; h+=2) {

    // compute yhat & xtdl
    for(int j = gg; j > 0; j-=1) {
      int16_t xavg = (x[j+h] + x[j+h+1]) / 2;  // use 2 audio samples
      yhat += (xavg*w[gg-j])/32768;
      xtdl += xavg*xavg;
    }

    error[h] = Mic[gg+h]-yhat;                 // apply same yhat to 2 samples
    error[h+1] = Mic[gg+h+1]-yhat;
    xtdl = xtdl + psi;
    mu0 = (67108864*mu)/xtdl;

    //update filter taps
    for(int j = 0; j < gg; j+=1){
      int xavg = (x[gg-j+h] + x[gg-j+h+1]) / 2;
      int erravg = (error[h] + error[h+1]) / 2;
      w[j] = w[j] + (xavg*mu0*erravg)/131072;
    }
  }

Can this allow "gg" to be half the size?
 
Status
Not open for further replies.
Back
Top