Low-latency two-level partitioned convolution for the T4

M

MarkT

Well-known member
This is an idea and code I've been working on for a while now, and its starting to get close to
completion, so I thought I'd highlight the kind of performance I'm seeing and the approach and
tricks used.

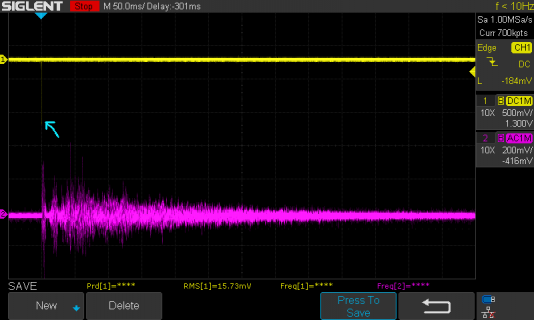
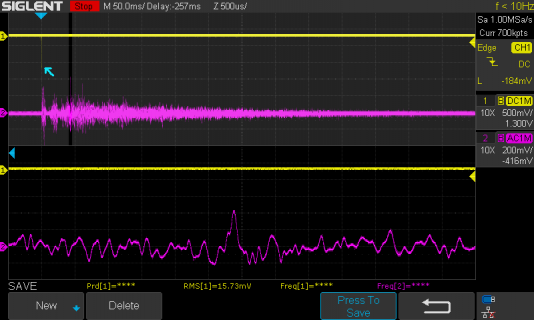
I've a 66161 sample (1.5s) impulse response on a 16bit WAV file on an SDcard. This is read in to configure
my class. This uses 404kB of dynamically allocated memory (DMAMEM I presume) in addition to
fixed buffers of 64kB in the class. This fits on a standard T4.

The algorithm uses two levels of uniformly-partitioned convolution spliced together, one that
processes the 128-sample audio blocks individually (achieving the 1 block latency), and one
that processes blocks of 2048 samples (16 times larger). There are 32 128-blocks handled
by tier1. And there are 31 2k-blocks handled by tier2 for this particular file. As tier2 only
needs to update every 46.4ms, this substantially reduces the processor cycles needed.

The tier2 processing is amortized over 16 consecutive update() calls to keep the CPU workload
even.

The result: I see about 28 to 35% ProcessorUsage on a T4.0 at 600MHz, which is very usable. (with
a single-tier partitioned convolution I could only get to 20k taps or so before the CPU usage started
to max-out)

This 35% is at 44100 sample rate at 66161 taps, mono. If this could be done in the time domain it
would only allow 0.34ns per multiply-accumulate operation.

One trick is to store the fft data as q15_t or q7_t arrays, despite the convolution processing all being
floating point, as this immediately reduces memory requirements a factor of 2 or more. The latter part of
the impulse response handled by tier2 uses only q7 storage for its filter fft data, using a per-block float
scaling factor to minimize quantization errors. This does entail some extra processing to re-scale however.

The sample fft data is kept at 16 bit in q15_t arrays, as this represents the signal itself. You can accept a
lot more raggedness in representing a reverberation impulse than the signal its modulating, I figure, especially
for the tail of the impulse response which is much lower in amplitude typically. The first 46ms of the impulse
response are entirely from the first tier at 16 bit resolution, thereafter it merges into the second tier with its
8-bit resolution.

Another trick is to use the real FFT primitives in CMSIS which use half the memory footprint for real
input (*)

This prevents the trick of coding two channels into the real and imaginary slots of a full complex FFT,
but I'm aiming for the most taps I can get.

The factor of 16 between the tiers is configurable, 16 seems to perform best for the larger impulse
responses - you want roughly equal block counts in the tiers for best throughput I think.


(*) actually this is only true for the arm_rfft_fast_f32 call, the others return a full spectrum.
 
Some 'scope shots of the input and output. I wrote an audio lib class to regularly output a single sample spike to
provoke the impulse response from the two-tier convolution, and 'scoped the input and output:

impulse_response.png

I've arrowed the very narrow spike on the input as its barely discernable. The trace covers only about
the first 0.65s from the total 1.5s of the response.

impulse_response_mag.png
The 100x expanded view to show the amount of detail - expanded trace is 0.5ms/div
 
The algorithm uses two levels of uniformly-partitioned convolution spliced together, one that
processes the 128-sample audio blocks individually (achieving the 1 block latency), and one
that processes blocks of 2048 samples (16 times larger). There are 32 128-blocks handled
by tier1. And there are 31 2k-blocks handled by tier2 for this particular file. As tier2 only
needs to update every 46.4ms, this substantially reduces the processor cycles needed.
Click to expand...

I am trying to better understand the application of convolution in audio processing. I am well versed in DSP theory regarding Convolution, FFTs, IFFTs, Impulse response , FIR filtering etc. but haven't specifically used Convolution in audio processing. I am also very familiar with and have used many of the DSP CMSIS Library functions. I would like to better understand the algorithm you are implementing in the Audio Library filter_twolev_partition.cpp and .h code. I see that you are starting with an impulse response that is 1.5sec in duration. How you use it to convolve the incoming signal is what I am trying understand.

@MARKT would it be possible to elaborate just a little on the process flow you are referencing in the paragraph quoted above? Or if their exists a link you can point me to that might show a similar process flow, it would really be appreciated. I realize this post is from over a year ago, but I was hoping I could get some help with my journey to apply convolution to audio processing. It is hard for me to understand the code without really some clarity around the process flow.

Thanks in advance for any help!
 
One way to convolve is to convert the signal and impulse-response to spectra using FFT, then multiple the FFT results point-by-point, then inverse FFT back to the time domain.
For large convolutions this becomes much more efficient as its N log N, not N^2.

There are ways to stitch blocks together doing this FFT-convolution so that it can be applied to an arbitrary length signal.

However you have a latency dependent on the size of the blocks.

So you make the blocks smaller and break up the impulse response into smaller pieces, and apply those pieces in parallel (you just have to sum the results). Then you can reduce the latency (but increase the cost - in the limit as you reduce the blocks down to 1 sample you converge on standard N^2 convolution).

You can do better with multiple sizes of block as the bulk of the impulse response can be done with larger blocks, only the initial parts using smaller blocks to keep the latency under control.

The key insights are the overlap-add and overlap-save methods of FFT convolution, plus the use of several block sizes, and the fact that different parts of a convolution can be processed independently and summed.
 
Thanks for the quick response. I read up on the overlap methods and uniform-partitioned convolution and believe I understand the approaches. This helps a lot. A few questions more if you have time please:

* You mentioned there wasn't enough uP horsepower to have all 128-block low latency uniform-partitioned convolution. That was the reason for the two tier approach. So does tier 1 represent processing the first 32 128-blocks and then you switch over to tier 2 processing of 21 2k-blocks? Or are they done in parallel somehow?
* I was going to try and run the examples you included in the Audio Library, but I couldn't find an example Impulse Response anywhere in the Library. Are you leaving that up to a user to generate/locate an IR to use? Or is it somewhere in the Audio Library that I missed?

Thanks again for you help. This is a fun topic.
 
The 2k block processing in done in small chunks so it can be scheduled with the small blocks and avoid large latency. Every 128 samples the processing for the new small blocks is done and a fraction of the processing for the large blocks - its messy, I don't remember the details, the code does though(!).

The impulse response is an input, so you have to find one or generate one.
 
Also, be sure that your IR uses minimum phase coefficients. Simply calculating linear phase coefficients works, but then the latency is still as long as the filter length/IR length. The whole trick of achieving low latency only works with minimal phase coefficients.
 
Thanks @MarkT for your help in understanding this. And thanks @DD4WH for the sample IRs and your clarification on using minimum phase coefficients for low latency.

Fun stuff!
 
I know this thread is a little bit old...

I tried to use your code, but it seems that it makes my Teensy 4.1 crash after a few seconds :

Code: 
#include <Audio.h>
#include <arm_const_structs.h>
#include <utility/imxrt_hw.h>
#include "filter_twolev_partition.h"

const int nc = 1280;
float32_t FIR_filter[nc];

AudioInputI2S               i2s_in; //communication I2S avec le micro
AudioOutputI2S              i2s_out; //communication I2S avec l'ampli
AudioFilterTwolevPart       convolution;

AudioConnection             patchCord_in(i2s_in, 0, convolution, 0);
AudioConnection             patchCord_out(convolution, 0, i2s_out, 0);

void setup() {

  AudioMemory(20);
  delay(100);

  digitalWrite(13,HIGH);
 
  for (int i = 0; i < nc; i++){
    if(i==0||i==nc/2){FIR_filter[i] = 1;}
    else{FIR_filter[i] = 0;}
  }

  AudioNoInterrupts() ;
  convolution.setFIRCoefficients(nc,FIR_filter);
  AudioInterrupts();

  delay(1000);
}

void loop() {}
 
Try adding the following at the top of your setup() function. If there is a crash, the report will be generated & displayed in the Serial Monitor.

Code: 
   unsigned long check_time;

   Serial.begin(57600);

   check_time = millis();
   while (!Serial && ((millis() - check_time) <= 3000));

   if (CrashReport)
   {
      Serial.print(CrashReport);
   }

Hope that helps . . .

Mark J Culross
KD5RXT
 
Its been a while since I used this, it might be a lack of memory (only the setSampleCount() function currently reports back a success value, the setFIRCoefficients() call blindly ignores if setSampleCount() fails - that needs fixing really, both should return bool...)
 
You must log in or register to reply here.
Back
Top