DD4WH
Well-known member
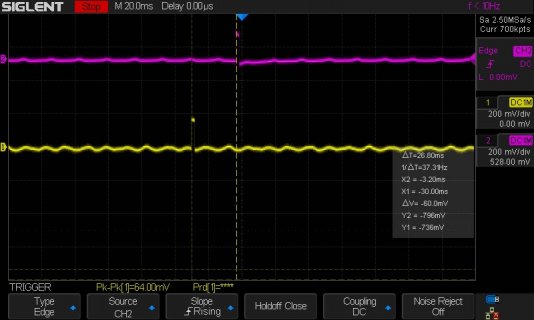
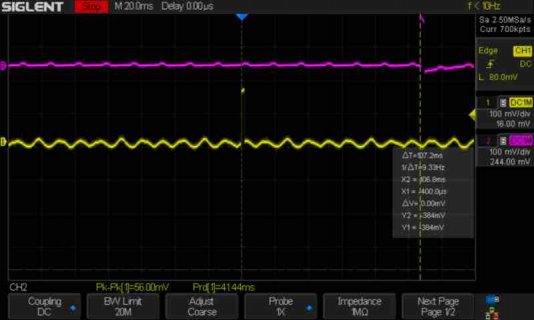
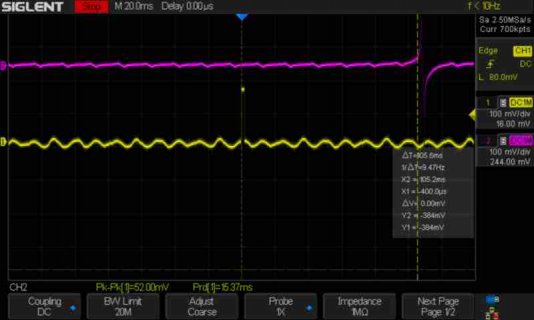
To test T4 performance I extracted the fast convolution filtering code from my SDR and tested it with the Teensy 4.0 and the Teensy audio board. Both were connected with flying wires (MCLK with 100ohms series resistor).
The code takes stereo I2S input and performs bandpass filtering of both channels simultaneously (in one complex FFT/cplxmultiply/iFFT operation) and outputs them as I2S output to the SGTL5000 outputs.
You can choose the FFT size (equivalent to steepness of the filter skirts / number of FIR filter taps). It uses fast convolution with overlap & save and 50% overlap and 4-term-Blackman-Harris-windowing. You can alter the FFT size [256, 512, 1024, 2048, 4096], which is equivalent to number of FIR taps [129, 513, 1025, 2049] and the FFT window. Also try to change the lower and upper bandpass cutoff frequency for the filter.
The filter response with a 4096-sized FFT has skirts so steep, that you will never want any larger filter response ;-).
The processor load is so amazingly low, that I can hardly believe it (they are output in the serial monitor). Maybe someone would be willing to check, if I did the math right in the sketch . . . Here are the figures:
Amazingly, the processor load does not differ much between the different FFT sizes and even drops when going from 1025 to 2049 FIR taps. However, memory usage is excessive!!! Can anybody explain this? It is not really fully explained by sum of the sizes of the assigned variables in the sketch . . .
All the best,
Frank DD4WH
P.S.: if the figures for the processor load are really calculated correctly, we would really have to think about using fast convolution filtering for even the smallest filtering tasks, eg. a parametric Equalizer, this could solve the problems associated with low frequency IIR filtering, for example.
Code:
/*
* just a small sketch to play around with audio processing with the Teensy 4
*
* FAST CONVOLUTION FILTERING in Stereo
*
* uses Teensy 4.0 and the Teensy audio board connected with flying wires
*
* Frank DD4WH 2019-08-17
*
* in the public domain GNU GPL
*/
#include <Audio.h>
#include <Wire.h>
#include <SPI.h>
#include <arm_math.h>
#include <arm_const_structs.h> // in the Teensy 4.0 audio library, the ARM CMSIS DSP lib is already a newer version
#define DEBUG
#define FOURPI (2.0 * TWO_PI)
#define SIXPI (3.0 * TWO_PI)
#define BUFFER_SIZE 128
int32_t sum;
int idx_t = 0;
float32_t mean;
int16_t *sp_L;
int16_t *sp_R;
uint8_t FIR_filter_window = 1;
uint8_t first_block = 1;
//double FLoCut = 150.0;
//double FHiCut = 4500.0;
double FLoCut = 5.0;
double FHiCut = 20000.0;
double SAMPLE_RATE = (double)AUDIO_SAMPLE_RATE_EXACT;
//const uint32_t FFT_L = 256;
//const uint32_t FFT_L = 512;
//const uint32_t FFT_L = 1024;
//const uint32_t FFT_L = 2048;
const uint32_t FFT_L = 4096;
double FIR_Coef_I[(FFT_L / 2) + 1]; // 2048 * 4 = 8kb
double FIR_Coef_Q[(FFT_L / 2) + 1]; // 2048 * 4 = 8kb
#define MAX_NUMCOEF (FFT_L / 2) + 1
uint32_t m_NumTaps = (FFT_L / 2) + 1;
uint32_t FFT_length = FFT_L;
const uint32_t N_B = FFT_L / 2 / BUFFER_SIZE;
uint32_t N_BLOCKS = N_B;
float32_t float_buffer_L [BUFFER_SIZE * N_B]; // 2048 * 4 = 8kb
float32_t float_buffer_R [BUFFER_SIZE * N_B]; // 2048 * 4 = 8kb
float32_t FFT_buffer [FFT_L * 2] __attribute__ ((aligned (4))); // 4096 * 4 = 16kb
float32_t last_sample_buffer_L [BUFFER_SIZE * N_B]; // 2048 * 4 = 8kb
float32_t last_sample_buffer_R [BUFFER_SIZE * N_B]; // 2048 * 4 = 8kb
// complex FFT with the new library CMSIS V4.5
const static arm_cfft_instance_f32 *S;
// complex iFFT with the new library CMSIS V4.5
const static arm_cfft_instance_f32 *iS;
float32_t iFFT_buffer [FFT_L * 2] __attribute__ ((aligned (4))); // 4096 * 4 = 16kb
// FFT instance for direct calculation of the filter mask
// from the impulse response of the FIR - the coefficients
const static arm_cfft_instance_f32 *maskS;
float32_t FIR_filter_mask [FFT_L * 2] __attribute__ ((aligned (4))); // 4096 * 4 = 16kb
// this audio comes from the codec by I2S
AudioInputI2S i2s_in;
AudioRecordQueue Q_in_L;
AudioRecordQueue Q_in_R;
AudioMixer4 mixleft;
AudioMixer4 mixright;
AudioPlayQueue Q_out_L;
AudioPlayQueue Q_out_R;
AudioOutputI2S i2s_out;
AudioControlSGTL5000 sgtl5000_1;
AudioConnection patchCord1(i2s_in, 0, Q_in_L, 0);
AudioConnection patchCord2(i2s_in, 1, Q_in_R, 0);
AudioConnection patchCord3(Q_out_L, 0, mixleft, 0);
AudioConnection patchCord4(Q_out_R, 0, mixright, 0);
AudioConnection patchCord9(mixleft, 0, i2s_out, 1);
AudioConnection patchCord10(mixright, 0, i2s_out, 0);
void setup() {
Serial.begin(115200);
delay(100);
AudioMemory(60); // must be high enough to deliver 16 stereo blocks = 32 * 128 samples at any point in time!
delay(100);
/****************************************************************************************
Audio Shield Setup
****************************************************************************************/
sgtl5000_1.enable();
sgtl5000_1.inputSelect(AUDIO_INPUT_LINEIN);
sgtl5000_1.adcHighPassFilterDisable(); // does not help too much!
sgtl5000_1.lineInLevel(14);
sgtl5000_1.lineOutLevel(24);
mixleft.gain(0, 1.0);
mixright.gain(0, 1.0);
sgtl5000_1.volume(0.5);
/****************************************************************************************
set filter bandwidth
****************************************************************************************/
// this routine does all the magic of calculating the FIR coeffs
calc_cplx_FIR_coeffs (FIR_Coef_I, FIR_Coef_Q, m_NumTaps, FLoCut, FHiCut, SAMPLE_RATE);
/****************************************************************************************
init complex FFTs
****************************************************************************************/
switch (FFT_length)
{
case 256:
S = &arm_cfft_sR_f32_len256;
iS = &arm_cfft_sR_f32_len256;
maskS = &arm_cfft_sR_f32_len256;
break;
case 512:
S = &arm_cfft_sR_f32_len512;
iS = &arm_cfft_sR_f32_len512;
maskS = &arm_cfft_sR_f32_len512;
break;
case 1024:
S = &arm_cfft_sR_f32_len1024;
iS = &arm_cfft_sR_f32_len1024;
maskS = &arm_cfft_sR_f32_len1024;
break;
case 2048:
S = &arm_cfft_sR_f32_len2048;
iS = &arm_cfft_sR_f32_len2048;
maskS = &arm_cfft_sR_f32_len2048;
break;
case 4096:
S = &arm_cfft_sR_f32_len4096;
iS = &arm_cfft_sR_f32_len4096;
maskS = &arm_cfft_sR_f32_len4096;
break;
}
/****************************************************************************************
Calculate the FFT of the FIR filter coefficients once to produce the FIR filter mask
****************************************************************************************/
init_filter_mask();
/****************************************************************************************
begin to queue the audio from the audio library
****************************************************************************************/
delay(100);
Q_in_L.begin();
Q_in_R.begin();
} // END OF SETUP
void loop() {
elapsedMicros usec = 0;
// are there at least N_BLOCKS buffers in each channel available ?
if (Q_in_L.available() > N_BLOCKS + 0 && Q_in_R.available() > N_BLOCKS + 0)
{
// get audio samples from the audio buffers and convert them to float
for (unsigned i = 0; i < N_BLOCKS; i++)
{
sp_L = Q_in_L.readBuffer();
sp_R = Q_in_R.readBuffer();
// convert to float one buffer_size
// float_buffer samples are now standardized from > -1.0 to < 1.0
arm_q15_to_float (sp_L, &float_buffer_L[BUFFER_SIZE * i], BUFFER_SIZE); // convert int_buffer to float 32bit
arm_q15_to_float (sp_R, &float_buffer_R[BUFFER_SIZE * i], BUFFER_SIZE); // convert int_buffer to float 32bit
Q_in_L.freeBuffer();
Q_in_R.freeBuffer();
}
/**********************************************************************************
Digital convolution
**********************************************************************************/
// basis for this was Lyons, R. (2011): Understanding Digital Processing.
// "Fast FIR Filtering using the FFT", pages 688 - 694
// numbers for the steps taken from that source
// Method used here: overlap-and-save
// ONLY FOR the VERY FIRST FFT: fill first samples with zeros
if (first_block) // fill real & imaginaries with zeros for the first BLOCKSIZE samples
{
for (unsigned i = 0; i < BUFFER_SIZE * N_BLOCKS; i++)
{
FFT_buffer[i] = 0.0;
}
first_block = 0;
}
else
{ // HERE IT STARTS for all other instances
// fill FFT_buffer with last events audio samples
for (unsigned i = 0; i < BUFFER_SIZE * N_BLOCKS; i++)
{
FFT_buffer[i * 2] = last_sample_buffer_L[i]; // real
FFT_buffer[i * 2 + 1] = last_sample_buffer_R[i]; // imaginary
}
}
// copy recent samples to last_sample_buffer for next time!
for (unsigned i = 0; i < BUFFER_SIZE * N_BLOCKS; i++)
{
last_sample_buffer_L [i] = float_buffer_L[i];
last_sample_buffer_R [i] = float_buffer_R[i];
}
// now fill recent audio samples into FFT_buffer (left channel: re, right channel: im)
for (unsigned i = 0; i < BUFFER_SIZE * N_BLOCKS; i++)
{
FFT_buffer[FFT_length + i * 2] = float_buffer_L[i]; // real
FFT_buffer[FFT_length + i * 2 + 1] = float_buffer_R[i]; // imaginary
}
/**********************************************************************************
Complex Forward FFT
**********************************************************************************/
// calculation is performed in-place the FFT_buffer [re, im, re, im, re, im . . .]
arm_cfft_f32(S, FFT_buffer, 0, 1);
/**********************************************************************************
Complex multiplication with filter mask (precalculated coefficients subjected to an FFT)
**********************************************************************************/
arm_cmplx_mult_cmplx_f32 (FFT_buffer, FIR_filter_mask, iFFT_buffer, FFT_length);
/**********************************************************************************
Complex inverse FFT
**********************************************************************************/
arm_cfft_f32(iS, iFFT_buffer, 1, 1);
/**********************************************************************************
Overlap and save algorithm, which simply means yóu take only the right part of the buffer and discard the left part
**********************************************************************************/
for (unsigned i = 0; i < FFT_length / 2; i++)
{
float_buffer_L[i] = iFFT_buffer[FFT_length + i * 2];
float_buffer_R[i] = iFFT_buffer[FFT_length + i * 2 + 1];
}
/**********************************************************************************
Demodulation / manipulation / do whatever you want
**********************************************************************************/
// at this time, just put filtered audio (interleaved format, overlap & save) into left and right channel
/**********************************************************************
CONVERT TO INTEGER AND PLAY AUDIO - Push audio into I2S audio chain
**********************************************************************/
for (int i = 0; i < N_BLOCKS; i++)
{
sp_L = Q_out_L.getBuffer();
sp_R = Q_out_R.getBuffer();
arm_float_to_q15 (&float_buffer_L[BUFFER_SIZE * i], sp_L, BUFFER_SIZE);
arm_float_to_q15 (&float_buffer_R[BUFFER_SIZE * i], sp_R, BUFFER_SIZE);
Q_out_L.playBuffer(); // play it !
Q_out_R.playBuffer(); // play it !
}
/**********************************************************************************
PRINT ROUTINE FOR ELAPSED MICROSECONDS
**********************************************************************************/
#ifdef DEBUG
sum = sum + usec;
idx_t++;
if (idx_t > 40) {
mean = sum / idx_t;
if (mean / 29.00 / N_BLOCKS * SAMPLE_RATE / AUDIO_SAMPLE_RATE_EXACT < 100.0)
{
Serial.print("processor load: ");
Serial.print (mean / 29.00 / N_BLOCKS * SAMPLE_RATE / AUDIO_SAMPLE_RATE_EXACT);
Serial.println("%");
}
else
{
Serial.println("100%");
}
Serial.print (mean);
Serial.print (" microsec for ");
Serial.print (N_BLOCKS);
Serial.print (" stereo blocks ");
Serial.print("FFT-length = "); Serial.print(FFT_length);
Serial.print("; FIR filter length = "); Serial.println(m_NumTaps);
idx_t = 0;
sum = 0;
}
#endif
} // end of audio process loop
/**********************************************************************************
Add button check etc. here
**********************************************************************************/
}
//////////////////////////////////////////////////////////////////////
// Call to setup complex filter parameters [can process two channels at the same time!]
// The two channels could be stereo audio or I and Q channel in a Software Defined Radio
// SampleRate in Hz
// FLowcut is low cutoff frequency of filter in Hz
// FHicut is high cutoff frequency of filter in Hz
// Offset is the CW tone offset frequency
// cutoff frequencies range from -SampleRate/2 to +SampleRate/2
// HiCut must be greater than LowCut
// example to make 2700Hz USB filter:
// SetupParameters( 100, 2800, 0, 48000);
//////////////////////////////////////////////////////////////////////
void calc_cplx_FIR_coeffs (double * coeffs_I, double * coeffs_Q, int numCoeffs, double FLoCut, double FHiCut, double SampleRate)
// pointer to coefficients variable, no. of coefficients to calculate, frequency where it happens, stopband attenuation in dB,
// filter type, half-filter bandwidth (only for bandpass and notch)
{
//calculate some normalized filter parameters
double nFL = FLoCut / SampleRate;
double nFH = FHiCut / SampleRate;
double nFc = (nFH - nFL) / 2.0; //prototype LP filter cutoff
double nFs = PI * (nFH + nFL); //2 PI times required frequency shift (FHiCut+FLoCut)/2
double fCenter = 0.5 * (double)(numCoeffs - 1); //floating point center index of FIR filter
for (int i = 0; i < numCoeffs; i++) //zero pad entire coefficient buffer
{
coeffs_I[i] = 0.0;
coeffs_Q[i] = 0.0;
}
//create LP FIR windowed sinc, sin(x)/x complex LP filter coefficients
for (int i = 0; i < numCoeffs; i++)
{
double x = (float32_t)i - fCenter;
double z;
if ( abs((double)i - fCenter) < 0.01) //deal with odd size filter singularity where sin(0)/0==1
z = 2.0 * nFc;
else
switch (FIR_filter_window) {
case 1: // 4-term Blackman-Harris --> this is what Power SDR uses
z = (double)sin(TWO_PI * x * nFc) / (PI * x) *
(0.35875 - 0.48829 * cos( (TWO_PI * i) / (numCoeffs - 1) )
+ 0.14128 * cos( (FOURPI * i) / (numCoeffs - 1) )
- 0.01168 * cos( (SIXPI * i) / (numCoeffs - 1) ) );
break;
case 2:
z = (double)sin(TWO_PI * x * nFc) / (PI * x) *
(0.355768 - 0.487396 * cos( (TWO_PI * i) / (numCoeffs - 1) )
+ 0.144232 * cos( (FOURPI * i) / (numCoeffs - 1) )
- 0.012604 * cos( (SIXPI * i) / (numCoeffs - 1) ) );
break;
case 3: // cosine
z = (double)sin(TWO_PI * x * nFc) / (PI * x) *
cos((PI * (float32_t)i) / (numCoeffs - 1));
break;
case 4: // Hann
z = (double)sin(TWO_PI * x * nFc) / (PI * x) *
0.5 * (double)(1.0 - (cos(PI * 2 * (double)i / (double)(numCoeffs - 1))));
break;
default: // Blackman-Nuttall window
z = (double)sin(TWO_PI * x * nFc) / (PI * x) *
(0.3635819
- 0.4891775 * cos( (TWO_PI * i) / (numCoeffs - 1) )
+ 0.1365995 * cos( (FOURPI * i) / (numCoeffs - 1) )
- 0.0106411 * cos( (SIXPI * i) / (numCoeffs - 1) ) );
break;
}
//shift lowpass filter coefficients in frequency by (hicut+lowcut)/2 to form bandpass filter anywhere in range
coeffs_I[i] = z * cos(nFs * x);
coeffs_Q[i] = z * sin(nFs * x);
}
}
void init_filter_mask()
{
/****************************************************************************************
Calculate the FFT of the FIR filter coefficients once to produce the FIR filter mask
****************************************************************************************/
// the FIR has exactly m_NumTaps and a maximum of (FFT_length / 2) + 1 taps = coefficients, so we have to add (FFT_length / 2) -1 zeros before the FFT
// in order to produce a FFT_length point input buffer for the FFT
// copy coefficients into real values of first part of buffer, rest is zero
for (unsigned i = 0; i < m_NumTaps; i++)
{
FIR_filter_mask[i * 2] = FIR_Coef_I [i];
FIR_filter_mask[i * 2 + 1] = FIR_Coef_Q [i];
}
for (unsigned i = FFT_length + 1; i < FFT_length * 2; i++)
{
FIR_filter_mask[i] = 0.0;
}
// FFT of FIR_filter_mask
// perform FFT (in-place), needs only to be done once (or every time the filter coeffs change)
arm_cfft_f32(maskS, FIR_filter_mask, 0, 1);
} // end init_filter_maskThe code takes stereo I2S input and performs bandpass filtering of both channels simultaneously (in one complex FFT/cplxmultiply/iFFT operation) and outputs them as I2S output to the SGTL5000 outputs.
You can choose the FFT size (equivalent to steepness of the filter skirts / number of FIR filter taps). It uses fast convolution with overlap & save and 50% overlap and 4-term-Blackman-Harris-windowing. You can alter the FFT size [256, 512, 1024, 2048, 4096], which is equivalent to number of FIR taps [129, 513, 1025, 2049] and the FFT window. Also try to change the lower and upper bandpass cutoff frequency for the filter.
The filter response with a 4096-sized FFT has skirts so steep, that you will never want any larger filter response ;-).
The processor load is so amazingly low, that I can hardly believe it (they are output in the serial monitor). Maybe someone would be willing to check, if I did the math right in the sketch . . . Here are the figures:
| FFT size | no. of FIR taps | processing time | no. of AUDIO Blocks | processor load | memory used |
| 256 | 129 | 69µsec | 1 | 2.38% | 160kbytes |
| 512 | 257 | 133µsec | 2 | 2.29% | 173kbytes |
| 1024 | 513 | 303µsec | 4 | 2.61% | 193kbytes |
| 2048 | 1025 | 639µsec | 8 | 2.75% | 234kbytes |
| 4096 | 2049 | 1249µsec | 16 | 2.69% | 316kbytes |
Amazingly, the processor load does not differ much between the different FFT sizes and even drops when going from 1025 to 2049 FIR taps. However, memory usage is excessive!!! Can anybody explain this? It is not really fully explained by sum of the sizes of the assigned variables in the sketch . . .
All the best,
Frank DD4WH
P.S.: if the figures for the processor load are really calculated correctly, we would really have to think about using fast convolution filtering for even the smallest filtering tasks, eg. a parametric Equalizer, this could solve the problems associated with low frequency IIR filtering, for example.
Last edited: